Dynamic 3D Physical Rope in Godot - Part2
In previous article, we solve the problem of generating PinJoint3D at the right places on the fly, given two PhysicsBody3D and how long the rope is.
In this article, we try to draw a 3D rope mesh alongside those PinJoint3D in global space.
ImmediateMesh and Curve3D
ImmediateMesh is a great fit because our rope is constantly updated in every physical frame. ImmediateMesh provides OpenGL 1.x style immediate mode API to draw mesh.
Godot also provides a class called Curve3D, representing what its name indicates. Combining these two classes we can draw our rope through following steps:
- After all
PinJoint3Ds are arranged at the right place during the rope generation, we save their positions along with two anchor positions into aCurve3D - In every physical frame, we update the points of curve according to the place of pinjoints and anchors, whose positions are already solved by game engine's physics.
- In every rendering frame, we draw a 3d rope using
ImmediateMeshwith the points in the curve.
Draw 3D rope from a Curve3D
For every point of the curve, we extrude the point to a circle. It's not a precise circle in parametric equation, but a approximate one constitued of discrete vertices as we are doing real time rendering instead of offline ray tracing.
The function below returns the points on the cross section circle from a point of curve. With the section_circle_resolution increases, the circle is more continous at the cost of performance.
func _generate_cross_section_circle_points(point: Vector3, next_point: Vector3) -> PackedVector3Array:
var points := PackedVector3Array()
var dir := next_point - point
var right := dir.cross(Vector3.UP).normalized()
var up := right.cross(dir).normalized()
for i in section_circle_resolution:
var phi = 2.0 * PI * float(i) / float(section_circle_resolution)
var local_point := Vector3(sin(phi) * radius, cos(phi) * radius, 0.0)
var global_point := point + right * local_point.x + up * local_point.y
points.push_back(global_point)
return points
After we have the points on the circle, we draw quads between sibling circles. A quad is just two triangles. Note that we deliver our vertices to ImmediateMesh clockwise. ( a[i], b[i], b[j] ) then ( a[i], b[j], a[j] ).
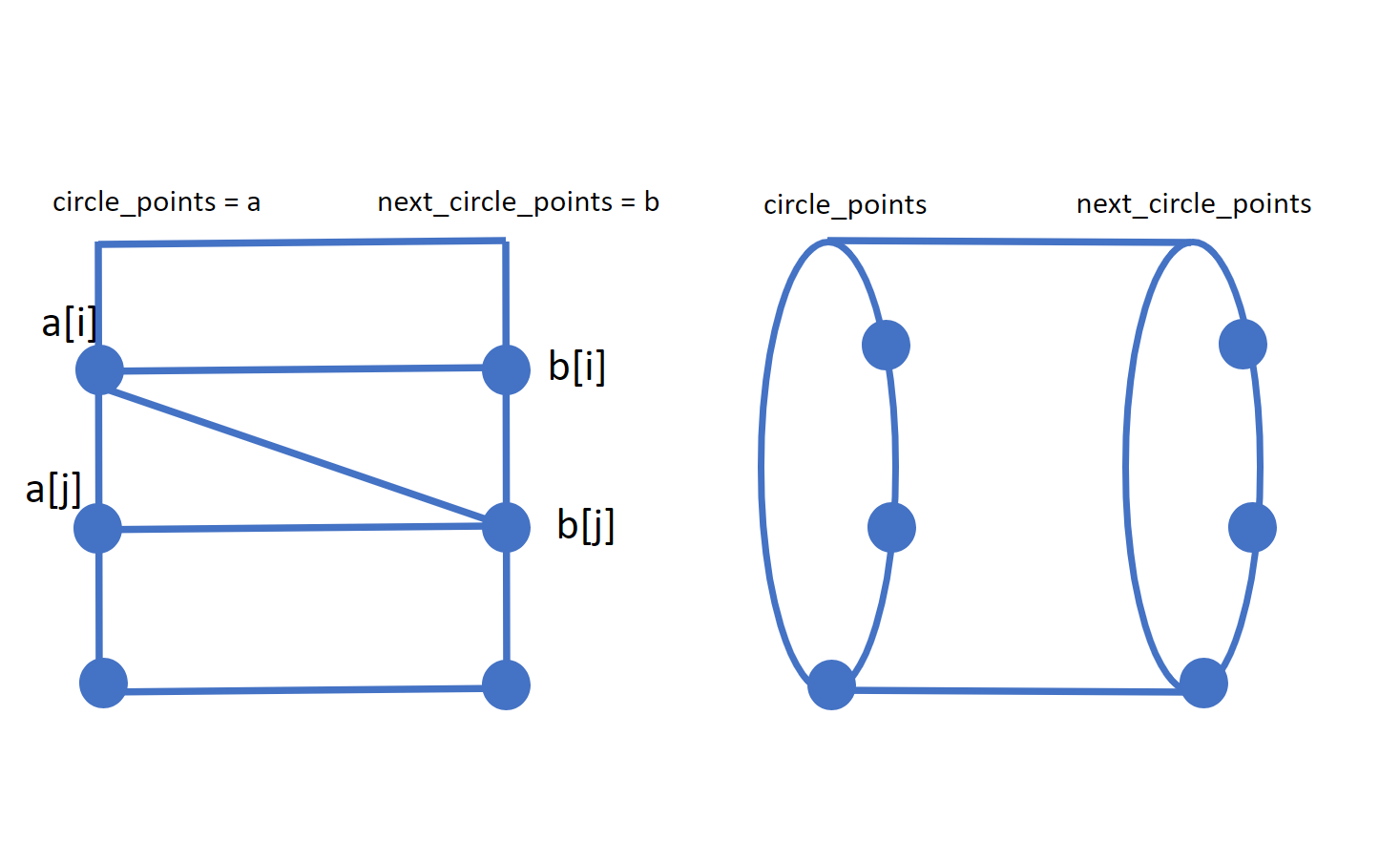
func _draw_quad_between_circle_points(circle_points: PackedVector3Array, next_circle_points: PackedVector3Array):
for i in section_circle_resolution:
var j := (i + 1) % section_circle_resolution
# First triangle
var i_normal := -1.0 * (circle_points[i] - circle_points[j]).cross(next_circle_points[i] - circle_points[i]).normalized()
mesh.surface_set_normal(i_normal)
mesh.surface_add_vertex(circle_points[i])
var next_i_normal := -1.0 * (circle_points[i] - next_circle_points[i]).cross(next_circle_points[i] - next_circle_points[j]).normalized()
mesh.surface_set_normal(next_i_normal)
mesh.surface_add_vertex(next_circle_points[i])
var next_j_normal := -1.0 * (circle_points[j] - next_circle_points[j]).cross(next_circle_points[i] - next_circle_points[j]).normalized()
mesh.surface_set_normal(next_j_normal)
mesh.surface_add_vertex(next_circle_points[j])
# Second triangle
mesh.surface_set_normal(i_normal)
mesh.surface_add_vertex(circle_points[i])
mesh.surface_set_normal(next_j_normal)
mesh.surface_add_vertex(next_circle_points[j])
var j_normal := -1.0 * (circle_points[i] - circle_points[j]).cross(next_circle_points[j] - circle_points[j]).normalized()
mesh.surface_set_normal(j_normal)
mesh.surface_add_vertex(circle_points[j])
For more detail, you can checkout the github repo, especially the source file rope_mesh.gd
Further Improvements
The repo still has a lot to do, like UVs and rewriting in native languages like Rust to support more pinjoints at the same time. More pinjoints we have, more real it feels and behaves.
Reference
https://docs.godotengine.org/en/stable/tutorials/3d/procedural_geometry/immediatemesh.html
https://docs.godotengine.org/en/stable/classes/class_curve3d.html