It's not hard to create a nice static physical rope using blender. However in some scenarios we have to create physical ropes at runtime. This article tries to solve the problem below:

Given two PhysicsBody3D and how long the rope is(the length is always longer than the distance between two bodies), connect them at runtime with a rope that reacts to physics system.

I solved this problem in an abandoned 3D space werewolf game project last year. Now I want to share with you how I do it.

Physical Rope Basics

Similar to fluid matter simulation, a continuous physical rope is often divided into discrete parts.

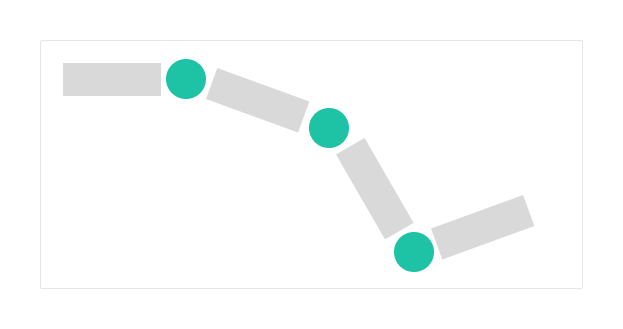
Each circle is a JointPin3D. Segment(rectangles in the image) will not be drawn as it is only actually abstract concept here(We will talk about the rendering in part 2). Each joint connects two neighbour joint or physical body. By using Joints, we get a physical rope of 6 degrees of freedom.

Tips: To make Joint work, we need at least one RigidBody3D

Inputs

In order to create the rope at runtime, we accept 4 inputs.

1. resolution: int, segments count. The higher this value, the more continuous this discrete simulation will feel like.
2. rope_length: float, how long the rope is. Of course this must be bigger than the distance between two anchors.
3. start_point: Node3D, a Node3D providing the information of global position of the starting anchor of the rope whose parent node is the physical body.
4. end_point: Node3D, same as above but provide the information of the ending anchor.

Overview

Basically we just need two steps:

1. Place segments correctly along the rope, we can easily calculate segment length from rope_length, and resolution which is joints count.
2. In each gap between every two segments, we put a joint right at it, connecting two neighbour segments.

Step 2 is fairly easy, we need to talk more on step 1.

Arrange the Positions of Segments

How to know the positions of segments even before we create them?

Well, we need to draw a line between two anchors, then arrange segments along this line evenly given segment_length and joint_length, where segment_length can be very small like 0.1 (Pinjoint3D will work the same whatever the initial distance is), joint_length = (rope_length - resolution * segment_length) / joint_count, joint_count = resolution + 1.

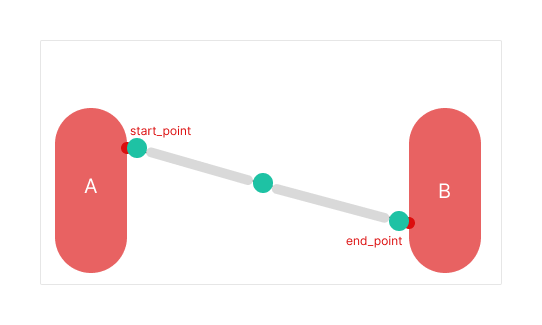
We place first and last joint at the position of start point and end point to let module user to customize.

As for situations where resolution is 1 or 2, the problem is much simpler.

When resolution is 1, there is only one segment connecting two joints.

When resolution is 2, joints count is 3, of which 2 are at anchors positions and segments count is 2(same as resolution). To make these 3 joints positioned evenly, just place the left one in the middle.

When resolution is greater than 2, things get interesting. As the rope length is longer than the distance, we must bend the line into two parts at a turning point. Let's say point T, and let's assume we need to connect body A and body B. The line is divided into two parts, one part is from body A to point T and the other one is from point T to body B. Then we just need to place pinjoints evenly along these two parts.

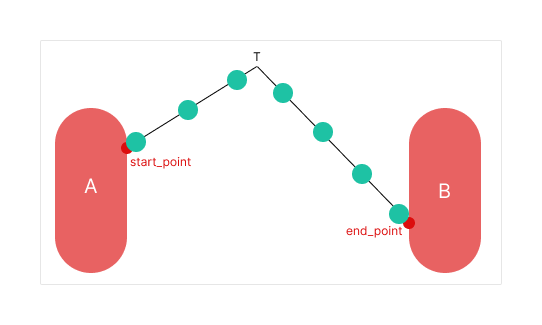
Now we need to calculate the global position of point T.

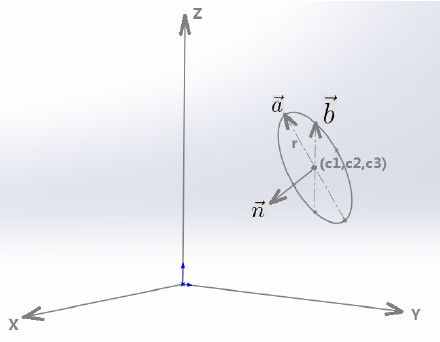
Suppose the length of part before T is r1, the length of part after T is r2. It is not hard to find that the trajectory of T is a circle, intersecting by two spheres whose radiuses are r1 and r2.

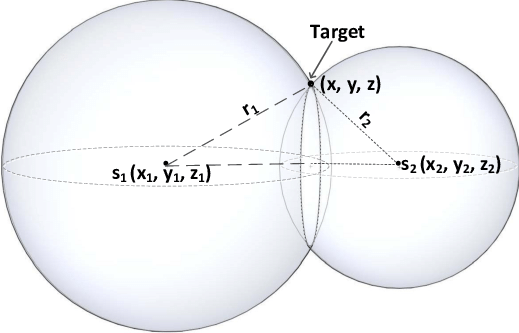
We already know:

1. two centers of the spheres, let's call them c1 and c2.
2. the normal of the intersecting circle, which is a vector between c1 and c2.
3. r1 and r2, we can approximately consider they are nearly half of the rope_length. If r1 does not equal r2 because of the parity of resolution, that's totally ok.

With parametric equations, we can solve this spatial circle.

where ) is the center of the circle, and are perpendicular unit vectors inside the circle, they are perpendicular to each other and perpendicular to the normal .

Here is the circle code:

class_name SphereSphereCircle
extends Object

var _rng = RandomNumberGenerator.new()

# spheres
var _sphere_a_center: Vector3
var _sphere_a_radius: float

var _sphere_b_center: Vector3
var _sphere_b_radius: float

var _sphere_sphere_distance: float


# triangle
var cosA: float
var a: float
var b: float
var c: float


# circle
var center: Vector3
var radius: float
var vector_a: Vector3
var vector_b: Vector3
var normal: Vector3


func _init(sphere_a_position: Node3D, sphere_a_radius: float, \
    sphere_b_position: Node3D, sphere_b_radius: float):
    _sphere_a_center = sphere_a_position.global_transform.origin
    _sphere_a_radius = sphere_a_radius
    _sphere_b_center = sphere_b_position.global_transform.origin
    _sphere_b_radius = sphere_b_radius
    _sphere_sphere_distance = _sphere_a_center.distance_to(_sphere_b_center)
    
    _calc_center()
    _calc_radius()
    _calc_vectors()


func _calc_center():    
    a = _sphere_b_radius
    b = _sphere_a_radius
    c = _sphere_sphere_distance
    cosA = (pow(b, 2) + pow(c, 2) - pow(a, 2)) / (2 * b * c)
    
    var k := b * cosA / c
    normal = _sphere_b_center - _sphere_a_center
    center = _sphere_a_center + k * normal


func _calc_radius():
    var sinA = sqrt(1 - pow(cosA, 2))
    radius = b * sinA


func _calc_vectors():
    var unit = Vector3.UP
    if not unit.cross(normal) == Vector3.ZERO:
        vector_a = unit.cross(normal).normalized()
    else:
        unit = Vector3.RIGHT
        vector_a = unit.cross(normal).normalized()

    vector_b = normal.cross(vector_a).normalized()


func get_point(theta: float) -> Vector3:
    var point := center + radius * cos(theta) * vector_a + radius * sin(theta) * vector_b
    return point

Initialize the circle, just randomize a theta between , and call get_point(theta), you get the global position of point T.

As we have point T, the rest of the work is just placing segments evenly alongside the bended line and connecting segments or phyiscal bodies with PinJoint3Ds.

Insert PinJoints

Now we have segments consisted of RopeSegment, each of them has correct global position. Now what we do is to connect them with PinJoint3Ds.

func _add_joints():
    var first_segment: RopeSegment = segments[0]
    var last_segment: RopeSegment = segments[resolution - 1]
    var first_joint = _generate_joint_between(head_anchor, first_segment)
    var last_joint = _generate_joint_between(last_segment, tail_anchor, 0)

    first_segment.add_child(first_joint)
    first_joint.global_transform.origin = start_point.global_transform.origin
    last_segment.add_child(last_joint)
    last_joint.global_transform.origin = end_point.global_transform.origin

    for i in len(segments):
        if segments.size() >= i + 2:
            var segment: RopeSegment = segments[i]
            var next_segment: RopeSegment = segments[i + 1]
            var joint = _generate_joint_between(segment, next_segment)
            segment.add_child(joint)
            var sphere_middle_point = segment.global_transform.origin + (next_segment.global_transform.origin - segment.global_transform.origin) * 0.5
            joint.global_transform.origin = sphere_middle_point

And _generate_joint_between() just setup the constraints for game engine's physics to resolve.

func _generate_joint_between(body_a: PhysicsBody3D, body_b: PhysicsBody3D, priority: int = 1) -> PinJoint3D:
    var joint := PinJoint3D.new()
    joint.set_node_a(body_a.get_path())
    joint.set_node_b(body_b.get_path())
    joint.set_solver_priority(priority)
    return joint

For more detail, you can checkout the github repo.

In next article, we will talk about the rendering part.

Reference

• https://www.zhihu.com/question/39049685
• https://blog.sina.com.cn/s/blog_6496e38e0102vi7e.html