计算机能解决的问题
一个数学问题是否有答案
十九世纪,数学家希尔伯特(Hilbert)一直在思考如下三个问题;
- 数学是完备的(complete)吗?所谓完备性,就是说对于任意一个命题,要么可以证明它是对的,要么可以证明它是错的。
- 数学是一致的(consistent)吗?所谓一致性,就是说一个命题不能既是真的,又是假的。
- 数学是可判定的(decisive)吗?所谓可判定性,就是说对于一个具体的问题,你能否判断它是否有答案。
希尔伯特的这三个问题从本质上划定了数学的边界。因为数学只能解决那些在数学上是完备的问题,而数学的一致性则能保证它没有似是而非的答案。希尔伯特自己没能回答这个问题。后来数学家哥德尔(Gödel)解决了前两个问题,提出了哥德尔不完全性定理:数学不可能既是完备的,又是一致的。关于第三个问题,希尔伯特提出了一个更为具体的问题,也就是希尔伯特第十题:对于任意多个未知数的整系数不定方程,要求给出一个可行的算法,使得借助于它,通过有限次运算,可以判断该方程有无整数解。举三个例子:
这个方程显然有整数解,它们就是勾股数,比如 345。
这是费马大定理的一个特例,由怀尔斯(Wiles)证明它无解。这个问题和上一个问题不论是有解还是无解,都是可判定的。
1970 年苏联数学家马季亚谢维奇(Matiyasevich)证明,对于这个方程,以及绝大多数不定方程,我们既不能证明它们有整数解,也无法证明解不存在。
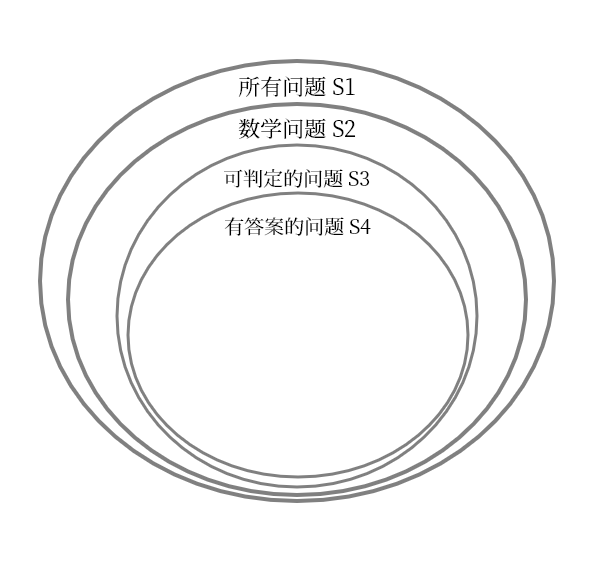
能否在有限步内找到答案
20 世纪 30 年代中期,图灵(Turing)开始思考下面三个本源问题:
- 数学问题是否都有明确的答案。
- 如果有明确的答案,是否可以通过有限步的计算得到答案。
- 对于那些有可能在有限步计算出来的数学问题,能否有一种假想的机器,它不断地运动,最后当它停下来地时候,那个数学问题就解决了。
图灵在 1936 年并不知道希尔伯特第十题的答案,但他猜测答案是否定的。所以他也给了自己三个问题中的前两个否定回答,即数学问题不是都有明确的答案,就算有明确的答案,也不能在有限步内得到答案。于是他将精力集中在可以在有限步内找到答案的问题。为此,他设计了一个数学模型,解决他提出的第三个问题。这个数学模型被后世称为图灵机。
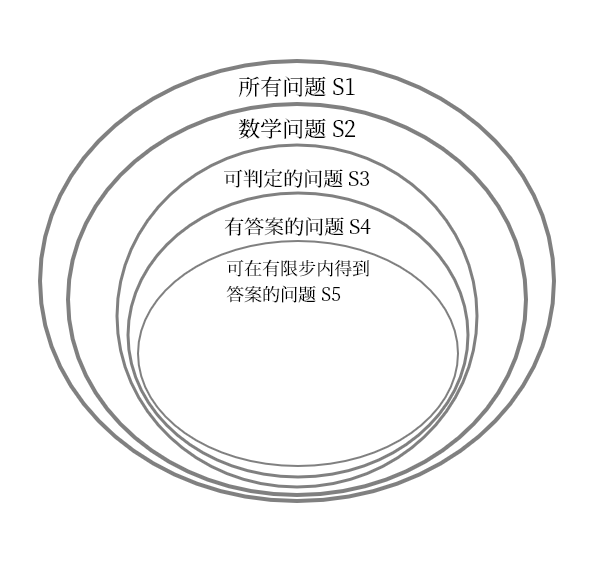
在上图 S5 中,有限步其实是图灵提出的理想假设。就算计算时间超过了宇宙的年龄,也还算有限步。比如计算复杂度等于或者超过指数函数的问题。所以在工程实践中,能解决的问题 S6 是 S5 的子集。
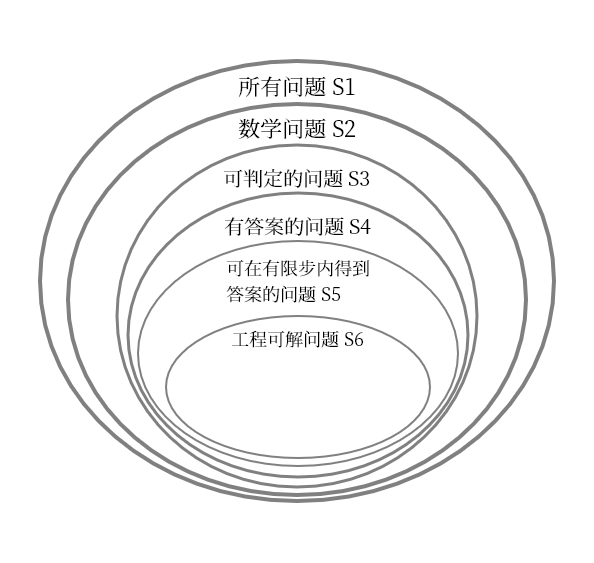
人工智能的极限
只要人工智能运行在计算机上,那么它所能解决的问题只是一个工程可解的问题的子集 S7。这几年人工智能显得越来越聪明,是因为人们发现了许多把一些特定问题转化成数学问题的方法,比如下围棋。S7 的外延有所扩大。但是 S7 永远不会超过 S6。
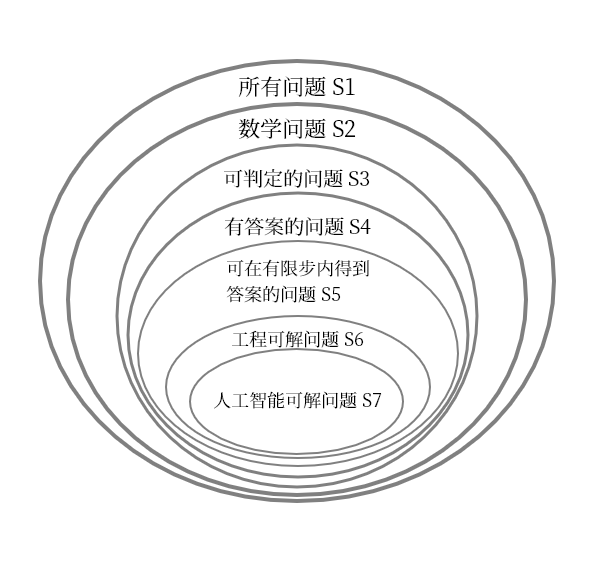
总结
计算机当初被发明就是用来解决数学问题,到今天,也只能解决图中的 S6。不论计算机的运算速度多么快,也无法达到 S5。比如,2018 年 Google 宣布他们的量子计算机可以破解现有的加密算法,好像我们的密码都变得不安全,但其实只要把密码长度加长一倍,计算机破解它的计算量就需要增加万亿倍。
可能存在解决非数学问题的机器,但是它不是我们今天所讨论的计算机。所谓的人工智能,所能解决的问题更是只有 S7。
巴菲特和芒格喜欢说能力圈(Ability Circle),作为个人,子曰五十而知天命,就是要认清楚自己能力的边界。超越理论边界的事情都是虚妄。